Chapter 7 -- Correlated samples in times, space, phylogeny... -- Exercise solutions and Code Boxes
David Warton
2022-08-24
Chapter7Solutions.RmdExercise 7.1: Biological control of aphids over time
Is there an effect of the netting treatment on changes in aphid numbers across the sampling times?
What sort of model is appropriate here?
Because we now have repeated measures in time, we have longitudinal data and should consider the methods of Section 7.1.1.
Code Box 7.1: R code to produce Figure 7.2.
library(ecostats)
data(aphids)
cols=c(rgb(1,0,0,alpha=0.5),rgb(0,0,1,alpha=0.5)) #transparent colours
par(mfrow=c(2,1),mar=c(3,3,1.5,1),mgp=c(2,0.5,0),oma=c(0,0,0.5,0))
with(aphids$oat, interaction.plot(Time,Plot,logcount,legend=FALSE,
col=cols[Treatment], lty=1, ylab="Counts [log(y+1) scale]",
xlab="Time (days since treatment)") )
legend("bottomleft",c("Excluded","Present"),col=cols,lty=1)
mtext("(a)",3,adj=0,line=0.5,cex=1.4)
with(aphids$oat, interaction.plot(Time,Treatment,logcount, col=cols,
lty=1, legend=FALSE, ylab="Counts [log(y+1) scale]",
xlab="Time (days since treatment)"))
legend("topright",c("Excluded","Present"),col=cols,lty=1)
mtext("(b)",3,adj=0,line=0.5,cex=1.4)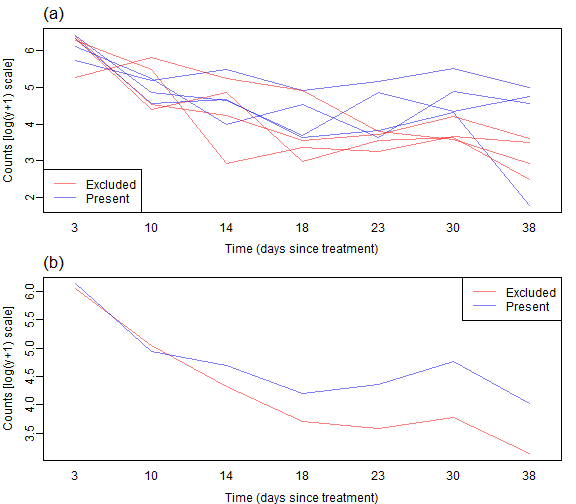
plot of chunk box71
Code Box 7.2: Choosing a longitudinal model for the aphid data
library(lme4)
aphid_int = lmer(logcount~Treatment*Time+Treatment*I(Time^2)+(1|Plot),
data=aphids$oat,REML=FALSE) # random intercepts model
aphid_slope = lmer(logcount~Treatment*Time+Treatment*I(Time^2)+(Time|Plot),
data=aphids$oat, REML=FALSE) # random slopes model
#> Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, : Model failed to
#> converge with max|grad| = 0.00715391 (tol = 0.002, component 1)
library(nlme) # refit random intercepts model in nlme to get a ACF:
aphid_int2 = lme(logcount~Treatment*Time+Treatment*I(Time^2),
random=~1|Plot, data=aphids$oat, method="ML")
plot(ACF(aphid_int2),alpha=0.05) # only works for nlme-fitted mixed models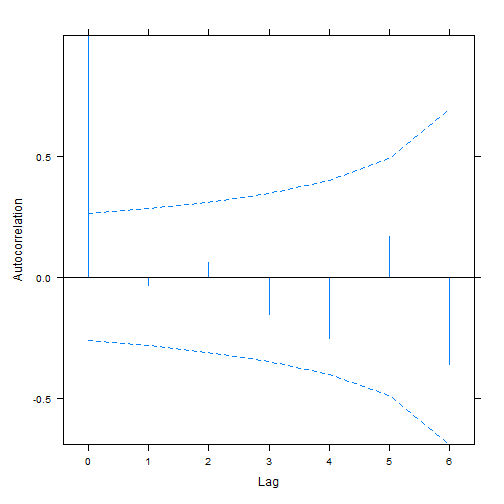
plot of chunk box72
Code Box 7.3: Exploring the random intercept fit to the aphids data
print(aphid_int)
#> Linear mixed model fit by maximum likelihood ['lmerMod']
#> Formula: logcount ~ Treatment * Time + Treatment * I(Time^2) + (1 | Plot)
#> Data: aphids$oat
#> AIC BIC logLik deviance df.resid
#> 128.3401 144.5429 -56.1701 112.3401 48
#> Random effects:
#> Groups Name Std.Dev.
#> Plot (Intercept) 0.202
#> Residual 0.635
#> Number of obs: 56, groups: Plot, 8
#> Fixed Effects:
#> (Intercept) Treatmentpresent Time
#> 6.5703718 -0.2379806 -0.1943256
#> I(Time^2) Treatmentpresent:Time Treatmentpresent:I(Time^2)
#> 0.0028708 0.0495183 -0.0004498
anova(aphid_int)
#> Analysis of Variance Table
#> npar Sum Sq Mean Sq F value
#> Treatment 1 2.0410 2.0410 5.0619
#> Time 1 24.7533 24.7533 61.3917
#> I(Time^2) 1 5.7141 5.7141 14.1717
#> Treatment:Time 1 1.6408 1.6408 4.0693
#> Treatment:I(Time^2) 1 0.0413 0.0413 0.1024
aphid_noTreat = lmer(logcount~Time+I(Time^2)+(1|Plot),
data=aphids$oat, REML=FALSE)
anova(aphid_noTreat,aphid_int)
#> Data: aphids$oat
#> Models:
#> aphid_noTreat: logcount ~ Time + I(Time^2) + (1 | Plot)
#> aphid_int: logcount ~ Treatment * Time + Treatment * I(Time^2) + (1 | Plot)
#> npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
#> aphid_noTreat 5 130.26 140.39 -60.131 120.26
#> aphid_int 8 128.34 144.54 -56.170 112.34 7.9224 3 0.04764 *
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Code Box 7.4: Exploring the random slopes fit to the aphids data
print(aphid_slope)
#> Linear mixed model fit by maximum likelihood ['lmerMod']
#> Formula: logcount ~ Treatment * Time + Treatment * I(Time^2) + (Time | Plot)
#> Data: aphids$oat
#> AIC BIC logLik deviance df.resid
#> 127.1708 147.4244 -53.5854 107.1708 46
#> Random effects:
#> Groups Name Std.Dev. Corr
#> Plot (Intercept) 0.11684
#> Time 0.01907 -1.00
#> Residual 0.57877
#> Number of obs: 56, groups: Plot, 8
#> Fixed Effects:
#> (Intercept) Treatmentpresent Time
#> 6.5703718 -0.2379806 -0.1943256
#> I(Time^2) Treatmentpresent:Time Treatmentpresent:I(Time^2)
#> 0.0028708 0.0495183 -0.0004498
#> optimizer (nloptwrap) convergence code: 0 (OK) ; 0 optimizer warnings; 1 lme4 warnings
anova(aphid_slope)
#> Analysis of Variance Table
#> npar Sum Sq Mean Sq F value
#> Treatment 1 0.7467 0.7467 2.2291
#> Time 1 12.8040 12.8040 38.2239
#> I(Time^2) 1 5.7141 5.7141 17.0582
#> Treatment:Time 1 0.8487 0.8487 2.5337
#> Treatment:I(Time^2) 1 0.0413 0.0413 0.1232
aphid_noTreatS = lmer(logcount~Time+I(Time^2)+(Time|Plot),
data=aphids$oat, REML=FALSE)
#> boundary (singular) fit: see help('isSingular')
anova(aphid_noTreatS,aphid_slope)
#> Data: aphids$oat
#> Models:
#> aphid_noTreatS: logcount ~ Time + I(Time^2) + (Time | Plot)
#> aphid_slope: logcount ~ Treatment * Time + Treatment * I(Time^2) + (Time | Plot)
#> npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
#> aphid_noTreatS 7 125.04 139.22 -55.519 111.04
#> aphid_slope 10 127.17 147.42 -53.585 107.17 3.8666 3 0.2762Exercise 7.2: Biological control of aphids in a wheat field
Repeat the above longitudinal analyses for data from the wheat field. Which longitudinal model better handles repeated measures in this case?
data(aphids)
cols=c(rgb(1,0,0,alpha=0.5),rgb(0,0,1,alpha=0.5)) #transparent colours
par(mar=c(3,3,1.5,1),mgp=c(2,0.5,0),oma=c(0,0,0.5,0))
with(aphids$wheat, interaction.plot(Time,Plot,logcount,legend=FALSE,
col=cols[Treatment], lty=1, ylab="Counts [log(y+1) scale]",
xlab="Time (days since treatment)") )
legend("bottomleft",c("Excluded","Present"),col=cols,lty=1)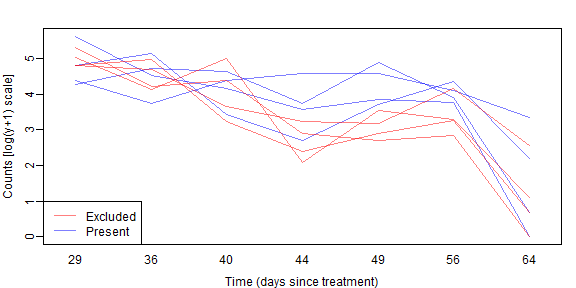
plot of chunk ex72plot
As before we don’t see a lot of lines crossing over so expect some correlation. We also see a similar pattern with aphid counts reducing over time, but possibly being higher without bird exclusion 2-5 weeks into the trial.
library(lme4)
aphidw_int = lmer(logcount~Treatment*Time+Treatment*I(Time^2)+(1|Plot),
data=aphids$wheat,REML=FALSE) # random intercepts model
#> Warning: Some predictor variables are on very different scales: consider rescaling
#> boundary (singular) fit: see help('isSingular')
aphidw_slope = lmer(logcount~Treatment*Time+Treatment*I(Time^2)+(Time|Plot),
data=aphids$wheat, REML=FALSE) # random slopes model
#> Warning: Some predictor variables are on very different scales: consider rescaling
#> boundary (singular) fit: see help('isSingular')
library(nlme) # refit random intercepts model in nlme to get a ACF:
aphidw_int2 = lme(logcount~Treatment*Time+Treatment*I(Time^2),
random=~1|Plot, data=aphids$wheat, method="ML")
plot(ACF(aphidw_int2),alpha=0.05) # only works for nlme-fitted mixed models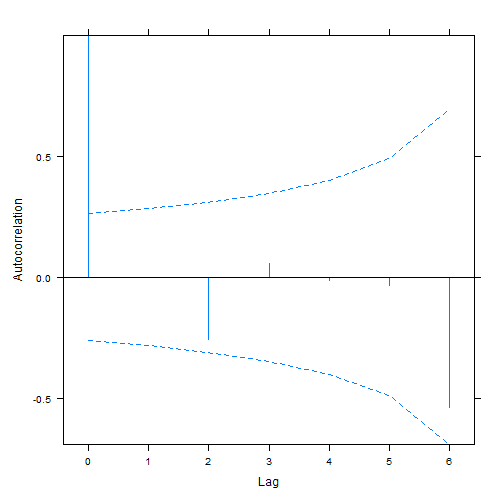
plot of chunk ex72long
# now try a model with a temporally structured random effect:
# for some reason this one returns non-convergence unless I make Tiem a (numerical) factor:
aphidsTimenFac=glmmTMB::numFactor(aphids$wheat$Time)
aphidw_CAR1 = update(aphidw_int2,correlation=corCAR1(,form=~aphidsTimenFac|Plot))
BIC(aphidw_int,aphidw_int2,aphidw_slope,aphidw_CAR1)
#> df BIC
#> aphidw_int 8 165.5916
#> aphidw_int2 8 165.5916
#> aphidw_slope 10 170.1048
#> aphidw_CAR1 9 169.6170As before the random intercept model seems to be favoured.
Is there evidence that bird exclusion improves biological control of aphids?
aphidw_noTr = lmer(logcount~Time+I(Time^2)+(1|Plot),
data=aphids$wheat,REML=FALSE) # random intercepts model
#> Warning: Some predictor variables are on very different scales: consider rescaling
#> boundary (singular) fit: see help('isSingular')
anova(aphidw_noTr,aphidw_int)
#> Data: aphids$wheat
#> Models:
#> aphidw_noTr: logcount ~ Time + I(Time^2) + (1 | Plot)
#> aphidw_int: logcount ~ Treatment * Time + Treatment * I(Time^2) + (1 | Plot)
#> npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
#> aphidw_noTr 5 151.02 161.15 -70.511 141.02
#> aphidw_int 8 149.39 165.59 -66.694 133.39 7.6327 3 0.05424 .
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1There is marginal evidence of a treatment effect.
Exercise 7.3: Biological control of aphids across both fields!
Construct a single, larger model to test for an effect of biological exclusion, and to check if this effect differs across fields.
aphids$oat$field = "oat"
aphids$wheat$field = "wheat"
aphids$wheat$Plot=paste0("W",aphids$wheat$Plot) #making sure we have different names for different Plots across fields
aphids$all = rbind(aphids$oat,aphids$wheat)
aphids$all$field = factor(aphids$all$field)
str(aphids$all)
#> 'data.frame': 112 obs. of 6 variables:
#> $ Plot : Factor w/ 16 levels "1","2","3","4",..: 1 2 3 4 5 6 7 8 1 2 ...
#> $ Treatment: Factor w/ 2 levels "excluded","present": 2 2 2 2 1 1 1 1 2 2 ...
#> $ Time : num 3 3 3 3 3 3 3 3 10 10 ...
#> $ counts : int 449 547 597 304 520 587 545 192 185 93 ...
#> $ logcount : num 6.11 6.31 6.39 5.72 6.26 ...
#> $ field : Factor w/ 2 levels "oat","wheat": 1 1 1 1 1 1 1 1 1 1 ...We will need a mixed model that allows effects to be different across fields (and times)
aphida_int = lmer(logcount~field*Time*Treatment+field*I(Time^2)*Treatment+(1|Plot),
data=aphids$all,REML=FALSE) # random intercepts model
#> Warning: Some predictor variables are on very different scales: consider rescaling
#> boundary (singular) fit: see help('isSingular')
aphida_noTr = lmer(logcount~field*Time+field*I(Time^2)+(1|Plot),
data=aphids$all,REML=FALSE) # random intercepts model
#> Warning: Some predictor variables are on very different scales: consider rescaling
anova(aphida_noTr,aphida_int)
#> Data: aphids$all
#> Models:
#> aphida_noTr: logcount ~ field * Time + field * I(Time^2) + (1 | Plot)
#> aphida_int: logcount ~ field * Time * Treatment + field * I(Time^2) * Treatment + (1 | Plot)
#> npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
#> aphida_noTr 8 280.88 302.63 -132.44 264.88
#> aphida_int 14 276.61 314.67 -124.30 248.61 16.273 6 0.01236 *
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1In the combined model there is some evidence of a treatment effect.
Exercise 7.4: Eucalypt richness as a function of the environment
Ian wanted to know: how does species richness vary from one area to the next, and what are the main environmental correlates of richness?… Plotting richness against spatial location, he found spatial clusters of high or low species richness (Fig. 7.3)… What sort of analysis method should Ian consider using?
He should be looking at fitting a spatial model, along the lines of Code Box 7.5.
Code Box 7.5: Model selection to choose predictors, and a spatial model, for Ian’s richness data
data(Myrtaceae)
Myrtaceae$logrich=log(Myrtaceae$richness+1)
ft_rich = lm(logrich~soil+poly(TMP_MAX,TMP_MIN,RAIN_ANN,degree=2),
data=Myrtaceae)
ft_richAdd = lm(logrich~soil+poly(TMP_MAX,degree=2)+
poly(TMP_MIN,degree=2)+poly(RAIN_ANN,degree=2), data=Myrtaceae)
BIC(ft_rich,ft_richAdd)
#> df BIC
#> ft_rich 19 1014.686
#> ft_richAdd 16 1002.806(The below code chunk takes several minutes to evaluate.)
library(nlme)
richForm = logrich~soil+poly(TMP_MAX,degree=2)+poly(TMP_MIN,degree=2)+
poly(RAIN_ANN,degree=2)
ft_richExp = gls(richForm,data=Myrtaceae,correlation=corExp(form=~X+Y))
ft_richNugg = gls(richForm,data=Myrtaceae,
correlation=corExp(form=~X+Y,nugget=TRUE))
BIC(ft_richExp,ft_richNugg)
#> df BIC
#> ft_richExp 17 1036.2154
#> ft_richNugg 18 979.5212Code Box 7.7: Spatial correlogram for Ian’s species richness data
library(pgirmess)
corRich = with(Myrtaceae,correlog(cbind(X,Y),logrich))
plot(corRich,xlim=c(0,150),ylim=c(-0.05,0.2))
abline(h=0,col="grey90")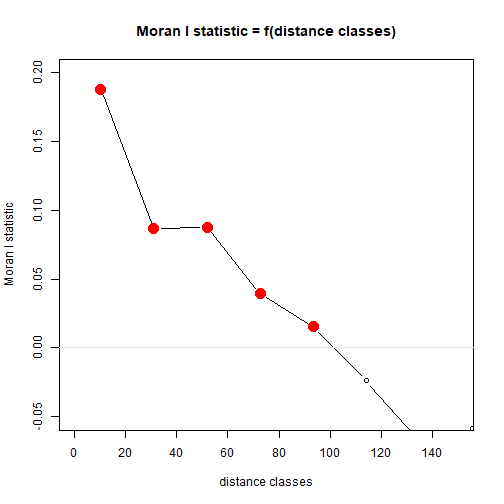
plot of chunk box77
Myrtaceae$resid = residuals(ft_richAdd)
corRichResid = with(Myrtaceae,correlog(cbind(X,Y),resid))
plot(corRichResid,xlim=c(0,150),ylim=c(-0.05,0.2))
abline(h=0,col="grey90")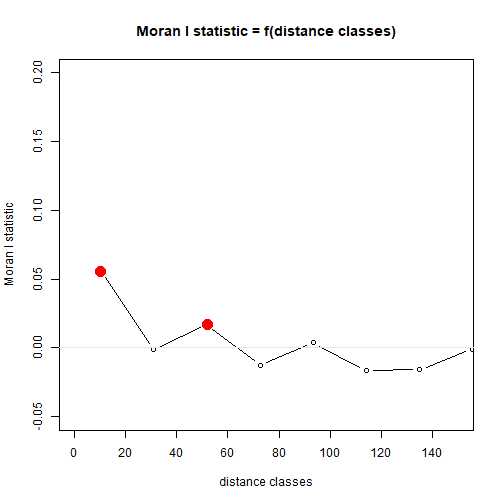
plot of chunk box77
Exercise 7.5: Egg size when Dads incubate
Terje wondered whether egg size was specifically limited by male body size. So he collected data on 71 species of shorebird where the male incubates the egg, measuring egg size, and size of adult males and females… What sort of model might be appropriate here?
We could try a linear model for egg size as a function of female and male bird size.
Can see you see any potential problems satisfying independence assumptions?
A potential issue is that there is a phylogenetic signal in many traits: if shorebird species are more closely related, we can expect their egg sizes to be more similar.
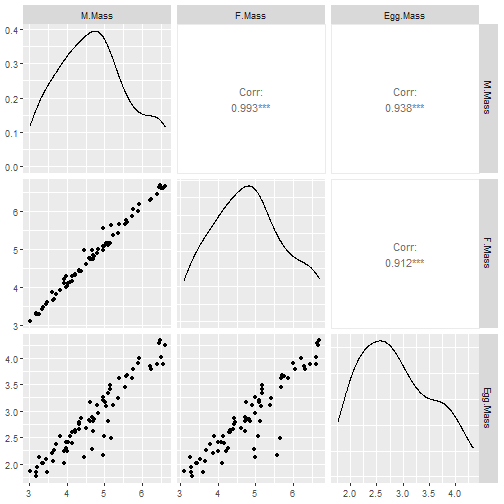
Code Box 7.8: Phylogenetic tree of 71 shorebird species
library(caper)
data(shorebird)
shore4d=phylobase::phylo4d(shorebird.tree,shorebird.data)
library(phylosignal)
barplot.phylo4d(shore4d,c("Egg.Mass","F.Mass","M.Mass"))
#> Warning in asMethod(object): trees with unknown order may be unsafe in ape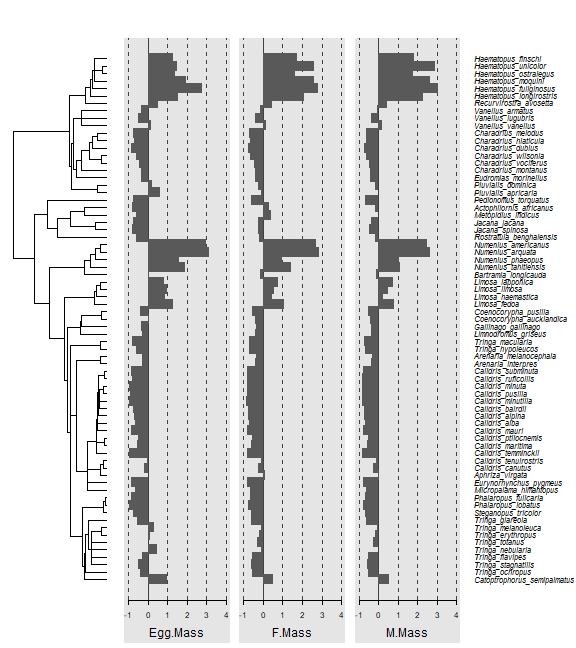
plot of chunk box7.8
Code Box 7.10: Comparative analysis of egg size data
library(caper)
shorebird = comparative.data(shorebird.tree, shorebird.data,
Species, vcv=TRUE)
pgls_egg = pgls(log(Egg.Mass) ~ log(F.Mass)+log(M.Mass),
data=shorebird)
summary(pgls_egg)
#>
#> Call:
#> pgls(formula = log(Egg.Mass) ~ log(F.Mass) + log(M.Mass), data = shorebird)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.097840 -0.027594 0.000748 0.018561 0.063632
#>
#> Branch length transformations:
#>
#> kappa [Fix] : 1.000
#> lambda [Fix] : 1.000
#> delta [Fix] : 1.000
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -0.37902 0.23172 -1.6357 0.106520
#> log(F.Mass) -0.22255 0.22081 -1.0079 0.317077
#> log(M.Mass) 0.89708 0.22246 4.0325 0.000142 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.03343 on 68 degrees of freedom
#> Multiple R-squared: 0.8476, Adjusted R-squared: 0.8431
#> F-statistic: 189.1 on 2 and 68 DF, p-value: < 2.2e-16Code Box 7.11: Residual diagnostics for egg size data
The below code chunk takes several minutes to evaluate so it has not been run
par(mfrow=c(2,2))
plot(pgls_egg)
res.df = data.frame(Species = shorebird.data$Species,
res = residuals(pgls_egg))
res4d = phylobase::phylo4d(shorebird.tree,res.df)
res.pg = phyloCorrelogram(res4d,trait="res")
plot(res.pg)Exercise 7.6: Comparative analysis of egg size data revisited
Refit the model allowing \(\lambda\) to be estimated from the data (using lambda="ML"), or allowing \(\delta\) to be estimated from the data.
pgls_eggL = pgls(log(Egg.Mass) ~ log(F.Mass)+log(M.Mass), lambda="ML",
data=shorebird)
summary(pgls_eggL)
#>
#> Call:
#> pgls(formula = log(Egg.Mass) ~ log(F.Mass) + log(M.Mass), data = shorebird,
#> lambda = "ML")
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.072175 -0.015738 0.001073 0.017126 0.057342
#>
#> Branch length transformations:
#>
#> kappa [Fix] : 1.000
#> lambda [ ML] : 0.947
#> lower bound : 0.000, p = 1.1224e-13
#> upper bound : 1.000, p = 0.033109
#> 95.0% CI : (0.839, 0.997)
#> delta [Fix] : 1.000
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -0.43469 0.20689 -2.1011 0.03934 *
#> log(F.Mass) -0.28756 0.22202 -1.2952 0.19963
#> log(M.Mass) 0.97556 0.22304 4.3740 4.293e-05 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.02841 on 68 degrees of freedom
#> Multiple R-squared: 0.8709, Adjusted R-squared: 0.8671
#> F-statistic: 229.3 on 2 and 68 DF, p-value: < 2.2e-16Does this change results and their interpretation?
Nope – results are pretty much the same as previously.
Now fit a linear model ignoring phylogeny, via lm. What happens here?
lm_egg = lm(log(Egg.Mass) ~ log(F.Mass)+log(M.Mass), data=shorebird.data)
summary(lm_egg)
#>
#> Call:
#> lm(formula = log(Egg.Mass) ~ log(F.Mass) + log(M.Mass), data = shorebird.data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.5843 -0.1104 0.0257 0.1338 0.4347
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -0.2105 0.1296 -1.624 0.109
#> log(F.Mass) -1.0605 0.2261 -4.691 1.36e-05 ***
#> log(M.Mass) 1.7433 0.2283 7.635 1.01e-10 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.2113 on 68 degrees of freedom
#> Multiple R-squared: 0.9089, Adjusted R-squared: 0.9063
#> F-statistic: 339.3 on 2 and 68 DF, p-value: < 2.2e-16The slopes move further from zero and everything becomes more significant. In particular, while there was no effect of female mass previously, now it is strongly significant.
Is this what you would expect?
Yes this is expected because phylogenetic relatedness introduces positive dependence, leading to under-estimation of uncertainty and a higher chance of false positives.
Look at the log-likelihood (using the logLik function) to help decide which of these models is a better fit to the data.
Something seems to be wrong with the df calculation in the pgls model, but the main thing to see here is that the log-likelihood is substantially higher for the pgls model, suggesting it is a much better fit to the data.